Scattering from a Sphere Under the Impedance
Boundary Condition
Abstract:
The scattering from a sphere is
analyzed by a Method of Moments, solving the Electric Field Integral
Equation with the Impedance Boundary Condition approximation. Results
are compared with the Mie theory.
Electric Field Integral Equation in case of the
Impedance Boundary Condition
For an homogeneous dielectric or conducting object, the scattering
problem
can be solved by the surface integral equation approach, involving
surface equivalent electric and magnetic currents. Such equation
enforce the boundary condition at the surface of the object of the
tangential component of the electric and magnetic field [2],
[1].
The application of the impedance boundary condition (IBC) results in
halving
the number of unknown, reducing the size of the matrix of the Method of
Moments and consequently reducing the computation time and the dinamic
memory required [3].
The impedance boundary condition states that the surface component
of
the electric 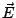 and magnetic
and magnetic 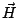 field are related by
field are related by
![$\displaystyle \vec E\vert _S \times \hat n = \zeta_c \left[\hat n \times (\vec H \times \hat n )\vert _S \right]$](img3.png) |
(1) |
where 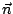 is the outer normal of the object surface
is the outer normal of the object surface 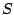 and the
and the
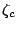 is the impedance of the object. Some
discussion about the
validity of the impedance boundary condition can be found in [4].
For homogeneous isotropic scatterers the limits of validity of the IBC
are:
being
is the impedance of the object. Some
discussion about the
validity of the impedance boundary condition can be found in [4].
For homogeneous isotropic scatterers the limits of validity of the IBC
are:
being 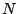 the refractive index of the object,
the refractive index of the object, 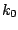 the wavenumber for the outside medium
and
the wavenumber for the outside medium
and 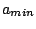 the smallest radius of curvature of the
surface of the object.
the smallest radius of curvature of the
surface of the object.
When the IBC can be applied, the equivalent surface electrical 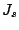 and
magnetical
and
magnetical 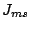 currents are related by
currents are related by
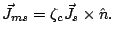 |
(4) |
The Electric Field Integral Equation (EFIE) can be written starting
from
eq. (1) and writing the tangential
component of the magnetic
field by the equivalent electric current
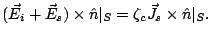 |
(5) |
where 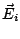 and
and 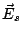 are the incident and
the scattered electric
field, respectively. Using the mixed potential to express the scattered
electric
field and the eq. 4, we obtain
are the incident and
the scattered electric
field, respectively. Using the mixed potential to express the scattered
electric
field and the eq. 4, we obtain
![$\displaystyle \begin{matrix}\hfill \hat n \times \vec E_i \vert _S = & \zeta_c ...
...t_{S} \vec J_{ms}(\vec r') g(\vec r, \vec r') dS' \right] . \hfill \end{matrix}$](img19.png) |
(6) |
with 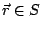 ,
, 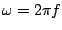 ,
, 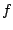 is the frequency,
is the frequency, 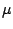 and
and
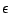 are the magnetic and the dielectric constant,
respectively, and
are the magnetic and the dielectric constant,
respectively, and
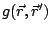 is the free spece
Green's function.
After the extraction of the singular point contribution
(
is the free spece
Green's function.
After the extraction of the singular point contribution
(
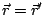 ) of the last term, we can write the EFIE as
) of the last term, we can write the EFIE as
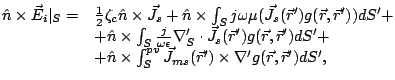 |
(7) |
where 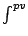 indicates that
the integral has to be
evaluated in its
principal value, and
indicates that
the integral has to be
evaluated in its
principal value, and 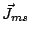 is related to the unknown equivalent
electric current
is related to the unknown equivalent
electric current 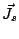 by eq. 4.
The eq. 7
is the EFIE that we solve with the Method of Moments.
by eq. 4.
The eq. 7
is the EFIE that we solve with the Method of Moments.
Once the electric equivalent current has been evaluated, the
scattered field
in the far region can be evaluated as [3]
![$\displaystyle \vec E_s(r,\theta,\phi) = \frac{e^{-jkr}}{r} \left[ F_1(\theta,\phi) \hat \theta + F_2(\theta,\phi) \hat \phi \right] ,$](img31.png) |
(8) |
where
Results
In the following we include some results, in terms of the bistatic
scattering
cross section, defined as
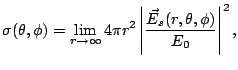 |
(11) |
normalized to the cross section (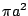 ) of a sphere of radius
) of a sphere of radius 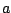 , with
, with 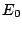 the intensity of the incident plane wave. The
results obtained by MoM with the IBC formulation are compared to those
obtained by the Mie series [3], for a
sphere with electrical radius
the intensity of the incident plane wave. The
results obtained by MoM with the IBC formulation are compared to those
obtained by the Mie series [3], for a
sphere with electrical radius
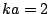 , and different values of the normalized impedance of the
medium
, and different values of the normalized impedance of the
medium
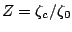 .
.
In order to apply the MoM, the Rao-Wilton-Glisson (RWG) basis
function
are used [5], with a sphere
discretized in triangles with an
approximate dimension of 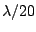 , for a mesh with 1078 nodes and
2152 triangles.
, for a mesh with 1078 nodes and
2152 triangles.
-
- 1
- J. J. H. Wang, Generalized Moment Methods in
Electromagnetics, John Wiley and Sons, 1991.
- 2
- K. Umashankar, A. Taflove, and S. M. Rao, ``Electromagnetic
scattering by arrbitrary shaped three-dimensional homogeneous lossy
dielectric objects,'' IEEE Trans. on Antennas and Propagat.,
vol. 34, 1986, pp. 758-766.
- 3
- A. Sebak, L. Shafai, ``Scattering from arbitrarily-shaped
objects with impedance boundary condition,'' IEE Proceedings, vol.
136, 1989, pp. 371-376.
- 4
- D. S. Wang, ``Limits and Validity of the Impedance Boundary
Condition on Penetrable Surfaces,'' IEEE Trans. on Antennas and
Propagat., vol. 35, 1987, pp.453-457.
- 5
- S. M. Rao, D. R. Wilton, A. W. Glisson, ``Electromagnetic
Scattering by Surfaces of Arbitrary Shape, IEEE Trans. on Antennas
and Propagat., vol. 30, 1982, pp. 409-418.
![]() and magnetic
and magnetic ![]() field are related by
field are related by
![]() and
magnetical
and
magnetical ![]() currents are related by
currents are related by
![$\displaystyle = -\frac{j\omega \mu_0}{4 \pi} \int_S \left[ \vec J_s(\vec r') \c...
... n(\vec r') \cdot \hat \phi(\theta,\phi) \right] e^{jk\hat r \cdot \vec r'} dS'$](img33.png)
![$\displaystyle = -\frac{j\omega \mu_0}{4 \pi} \int_S \left[ \vec J_s(\vec r') \c...
...vec r') \cdot \hat \theta(\theta,\phi) \right] e^{jk\hat r \cdot \vec r'} dS' .$](img35.png)
![]() , for a mesh with 1078 nodes and
2152 triangles.
, for a mesh with 1078 nodes and
2152 triangles.